Formal Decision Theory Is an Optional Tool That Breaks When Values are Huge

Formal decision theory is a tool -- a tool that breaks, a tool we can do without, a tool we optionally deploy and can sometimes choose to violate without irrationality.  If it leads to paradox or bad results, we can say "so much the worse for formal decision theory", moving on without it, as of course humans have done for almost all of their history.

I am inspired to these thoughts after reading Nick Beckstead and Turuji Thomas's recent paper in Nous, "A Paradox for Tiny Probabilities and Enormous Values".

Beckstead and Thomas lay out the following scenario:

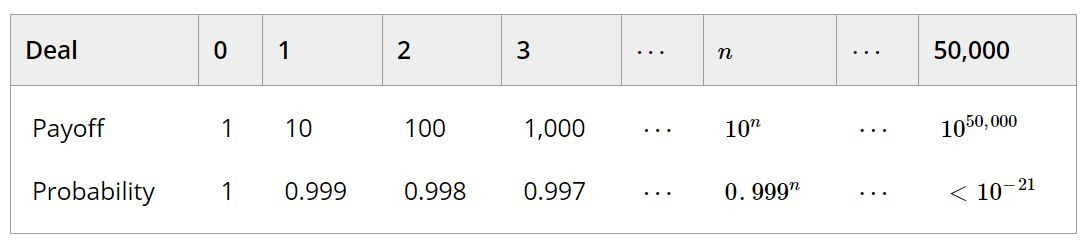
On your deathbed, God brings good news. Although, as you already knew, there's no afterlife in store, he'll give you a ticket that can be handed to the reaper, good for an additional year of happy life on Earth. As you celebrate, the devil appears and asks, ‘Won't you accept a small risk to get something vastly better? Trade that ticket for this one: it's good for 10 years of happy life, with probability 0.999.’ You accept, and the devil hands you a new ticket. But then the devil asks again, ‘Won't you accept a small risk to get something vastly better? Trade that ticket for this one: it is good for 100 years of happy life—10 times as long—with probability 0.999^2—just 0.1% lower.’ An hour later, you've made 10^50,000 trades. (The devil is a fast talker.) You find yourself with a ticket for 10^50,000  years of happy life that only works with probability .999^50,000, less than one chance in 10^21. Predictably, you die that very night. 

Here are the deals you could have had along the way:

On the one hand, each deal seems better than the one before. Accepting each deal immensely increases the payoff that's on the table (increasing the number of happy years by a factor of 10) while decreasing its probability by a mere 0.1%. It seems unreasonably timid to reject such a deal. On the other hand, it seems unreasonably reckless to take all of the deals—that would mean trading the certainty of a really valuable payoff for all but certainly no payoff at all. So even though it seems each deal is better than the one before, it does not seem that the last deal is better than the first.

Beckstead and Thomas aren't the first to notice that standard decision theory yields strange results when faced with tiny probabilities of huge benefits: See the literature on Pascal's Wager, Pascal's Mugging, and Nicolausian Discounting.

The basic problem is straightforward: Standard expected utility decision theory suggests that given a huge enough benefit, you should risk almost certainly destroying everything.  If the entire value of the observable universe is a googol (10^100) utils, then you should push a button that has a 99.999999999999999999999% chance of destroying everything as long as there is (or you believe that there is) a 0.00000000000000000000001% chance that it will generate more than 10^123 utils.

As Beckstead and Thomas make clear, you can either accept this counterintuitive conclusion (they call this recklessness) or reject standard decision theory.  However, the nonstandard theories that result are either timid (sometimes advising us to pass up an arbitrarily large potential gain to prevent a tiny increase in risk) or non-transitive (denying the principle that, if A is better than B and B is better than C, then A must be better than C).  Nicolausian Discounting, for example, which holds that below some threshold of improbability (e.g., 1/10^30), any gain no matter how large should be ignored, appears to be timid.  If a tiny decrease in probability would push some event below the Nicolausian threshold, then no potential gain could justify taking a risk or paying a cost for the sake of that event.

Beckstead and Thomas present the situation as a trilemma between recklessness, timidity, and non-transitivity.  But they neglect one horn.  It's actually a quadrilemma between recklessness, timidity, non-transitivity, and rejecting formal approaches to decision.

I recommend the last horn.  Formal decision theory is a limited tool, designed to help with a certain type of decision.  It is not, and should not be construed to be, a criterion of rationality.

Some considerations that support treating formal decision theory as a tool of limited applicability:

• If any one particular approach to formal decision theory were a criterion of rationality such that defying its verdicts were always irrational, then applying any other formal approach to decision theory (e.g., alternative approaches to risk) would be irrational.  But it's reasonable to be a pluralist about formal approaches to decision.

• Formal theories in other domains break outside of their domain of application.  For example, physicists still haven't reconciled quantum mechanics and general relativity.  These are terrific, well confirmed theories that seem perfectly general in their surface content, but it's reasonable not to apply both of them to all physical predictive or explanatory problems.

• Beckstead and Thomas nicely describe the problems with recklessness (aka "fanaticism") and timidity -- and denying transitivity also seems very troubling in a formal context.  Problems for each of those three horns of the quadrilemma is pressure toward the fourth horn.

• People have behaved rationally (and irrationally) for hundreds of thousands of years.  Formal decision theory can be seen as a model of rational choice.  Models are tools employed for a range of purposes; and like any model, it's reasonable to expect that formal decision theory would distort and simplify the target phenomenon.

• Enthusiasts of formal decision theory often already acknowledge that it can break down in cases of infinite expectation, such as the St. Petersburg Game -- a game in which a which a fair coin is flipped until it lands heads for the first time, paying 2^n, where n is the number of flips, yielding 2 if H, 4 if TH, 8 if TTH, 16 if TTTH, etc. (the units could be dollars or, maybe better, utils).  The expectation of this game is infinite, suggesting unintuitively that people should be willing to pay any cost to play it and also, unintuitively, that a variant that pays $1000 plus 2^n would be of equal value to the standard version that just pays 2^n.  Some enthusiasts of formal decision theory are already committed to the view that it isn't a universally applicable criterion of rationality.

In a 2017 paper and my 2024 book (only $16 hardback this month with Princeton's 50% discount!), I advocate a version of Nicolausian discounting.  My idea there -- though I probably could have been clearer about this -- was (or should have been?) not to advocate a precise, formal threshold of low probability below which all values are treated as zero while otherwise continuing to apply formal decision theory as usual.  (I agree with Monton and Beckstead and Thomas that this can lead to highly unintuitive results.)  Instead, below some vague-boundaried level of improbability, decision theory breaks and we can rationally disregard its deliverances.

As suggested by my final bullet point above, infinite cases cause at least as much trouble.  As I've argued with Jacob Barandes (ch. 7 of Weirdness, also here), standard physical theory suggests that there are probably infinitely many good and bad consequences of almost every action you perform, and thus the infinite case is likely to be the actual case: If there's no temporal discounting, the expectation of every action is ∞ + -∞.  We can and should discount the extreme long-term future in our decision making much as we can and should discount extremely tiny probabilities.  Such applications take formal decision theoretical models beyond the bounds of their useful application.  In such cases, it's rational to ignore what the formal models tell us.

Ah, but then you want a precise description of the discounting regime, the thresholds, the boundaries of applicability of formal decision theory?  Nope!  That's part of what I'm saying you can't have.